A tentative step into the worlds of asymmetric encryption and Blockchain
Disclaimer: This is not an in-depth overview of encryption and data management, more a slice of the concepts I've come across as a relative newcomer to this world (i.e. I'm new, please forgive my relative ignorance).
A brief introduction to hashing
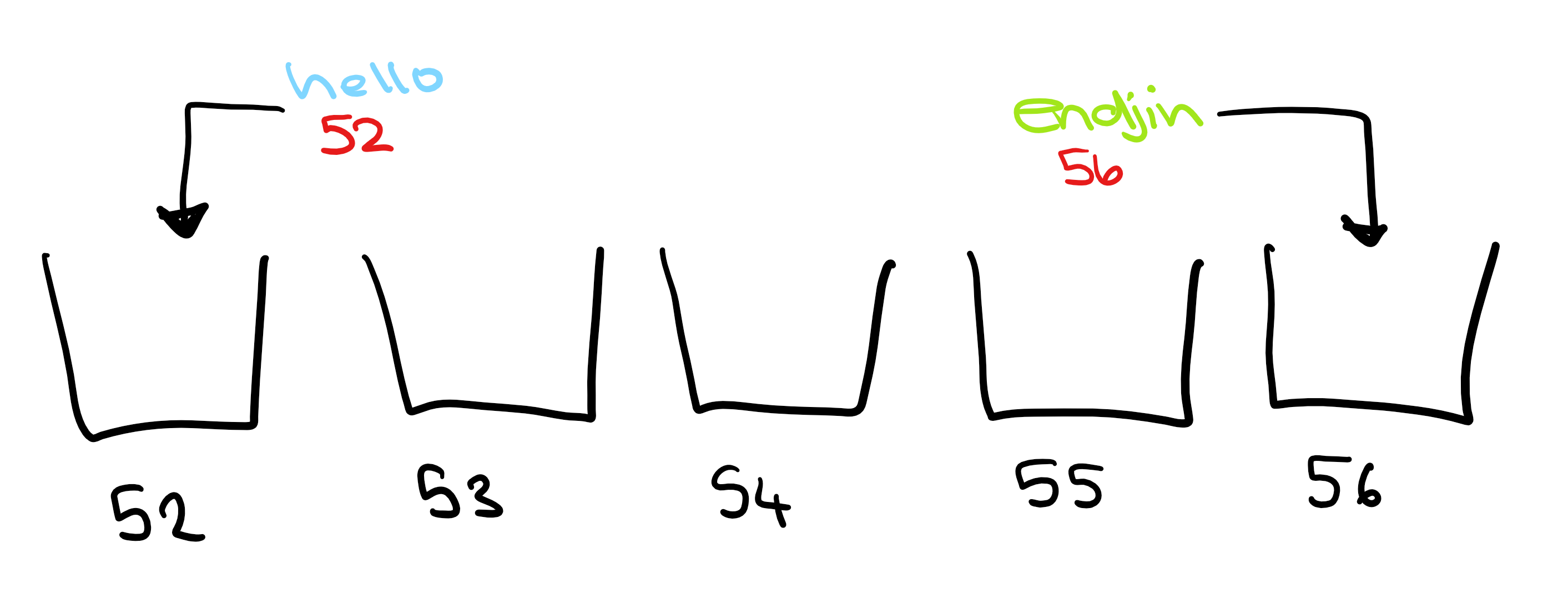
In order to talk about cryptography, we first need to understand hashing. In a very simple hashing algorithm, you could replace each letter in a word with its position in the alphabet, and sum these to get a hash representing the word. So:
hello = 8+5+12+12+15 = 52
endjin = 5+14+4+10+9+14 = 56
(I tried to add these numbers up mentally for a solid minute before resignedly opening the calculator app...)
Hashing is the mechanism which underlies the fast look up of the dictionary class in .NET. Each object which is added to the dictionary is passed through a hashing algorithm (though generally one more complex than shown here) and placed into a "bucket" which corresponds to a set of hash values.
When establishing if a dictionary contains an object, the object is passed through the algorithm, telling the dictionary which bucket to search. This means that not every entry needs to be searched to establish whether that object is present.
E.g. If you defined the Person class as follows:
private class Person : IEquatable<Person>
{
public readonly string firstName;
public readonly string lastName;
public readonly string fullName;
public Person(string firstName, string lastName)
{
this.firstName = firstName;
this.lastName = lastName;
this.fullName = firstName + " " + lastName;
}
public override bool Equals(object otherPerson)
{
if (otherPerson == null)
{
return false;
}
if (!(otherPerson.GetType() != typeof(Person)) {
return false;
}
return this.fullName == otherPerson.fullName;
}
// This overrides the GetHashCode() method of the Object class
public override int GetHashCode()
{
var sum = 0;
foreach (var character in this.fullName)
{
// This line gets the letter's position in the alphabet using the ASCII position
if (character != ' ')
{
sum += char.ToUpper(character) - 64;
}
}
return sum;
}
}
Here we are stating that two people with the same full name are equal. This may be problematic, though in my case perhaps not a ridiculous assumption. (If anyone knows any other Carmel Eves tell them to give me a shout and perhaps I'll revise this example!) If we then define a dictionary to relate people to their favourite colour:
var favouriteColourDictionary = new Dictionary<Person, string>();
var me = new Person("Carmel", "Eve");
favouriteColourDictionary.Add(me, "orange");
Then the GetHashCode method will be run, and the person & colour combination will be placed into the corresponding bucket, in this case: 3+1+18+13+5+12+5+22+5 = 84. Defining the hash code in this way is important because, in order to use a dictionary correctly, two objects which are defined as equal must produce the same hash code.
When you check if a dictionary contains a key:
var anotherMe = new Person("Carmel","Eve");
favouriteColourDictionary.ContainsKey(anotherMe);
The object's GetHashCode method is run, and the dictionary checks the corresponding bucket. So, if the object produces a different hash code to an object that it is equal to, the dictionary will be checking in the wrong bucket. So, using our GetHashCode definition, when this line is executed the dictionary will know to search bucket 84. It will then check the entries in that bucket using the Equals method and will find that the value is present. This also means that look-up is fast as it does not need to search all our other theoretical entries to check if the value is present. A word of warning: it is generally considered bad practice to change an object's Equals method, without also overriding the == / != operators, I have just left it out here to avoid cluttering the code.
Side note, it is okay *(*and in the case of e.g. strings where there is an almost limitless amount of possible combinations, unavoidable) to have a hashing algorithm that produces the same hashcode for multiple objects as they will just end up in the same bucket. However it is still best to keep this to a minimum as this will improve performance (as there will be fewer entries to search in each bucket), and in the wider world of hashing it is best avoided as much as possible.
But... My simple "algorithm" is hardly a good example of the hashing used in encryption.
Asymmetric cryptography
For cryptography, the most important aspect of a hashing algorithm is that it is effectively impossible to have any predictable control over the hash value. There must be no way in which to modify the input in order to create a desired hash, otherwise there can be no guarantee that the information has not been altered. So, though hashing is an integral part of cryptography, it is a very different beast to the previous example.
Asymmetric cryptography involves two keys: a public and a private one. As the names suggest, a public key is available publicly, to anyone that wants access. The private key however needs to be kept secret.
The public and private key are mathematically related. For example, in the Rivest–Shamir–Adleman (RSA) cryptosystem the public key is the product of two very large prime numbers, and the private key is those numbers themselves. This is secure due to the fact that finding large prime factors of large numbers is extremely computationally expensive. This relation means that it is possible to create an encryption algorithm by which something can be encrypted using someone's public key, and then can only be decrypted using their private and vice versa. In this way, you can send secure messages to someone and be safe in the knowledge that they are the only ones that will be able to decrypt it.
For clarity:
- Hashing is the production of (usually) a string of numbers from a string of text. A small change in the input string should produce a large change in the hash. They are also designed with the aim of being extremely difficult to return to the original value.
- **Encryption **is also the production of a string of numbers from string of text. However, these are designed so that, using the right key, they can be returned to their original value.
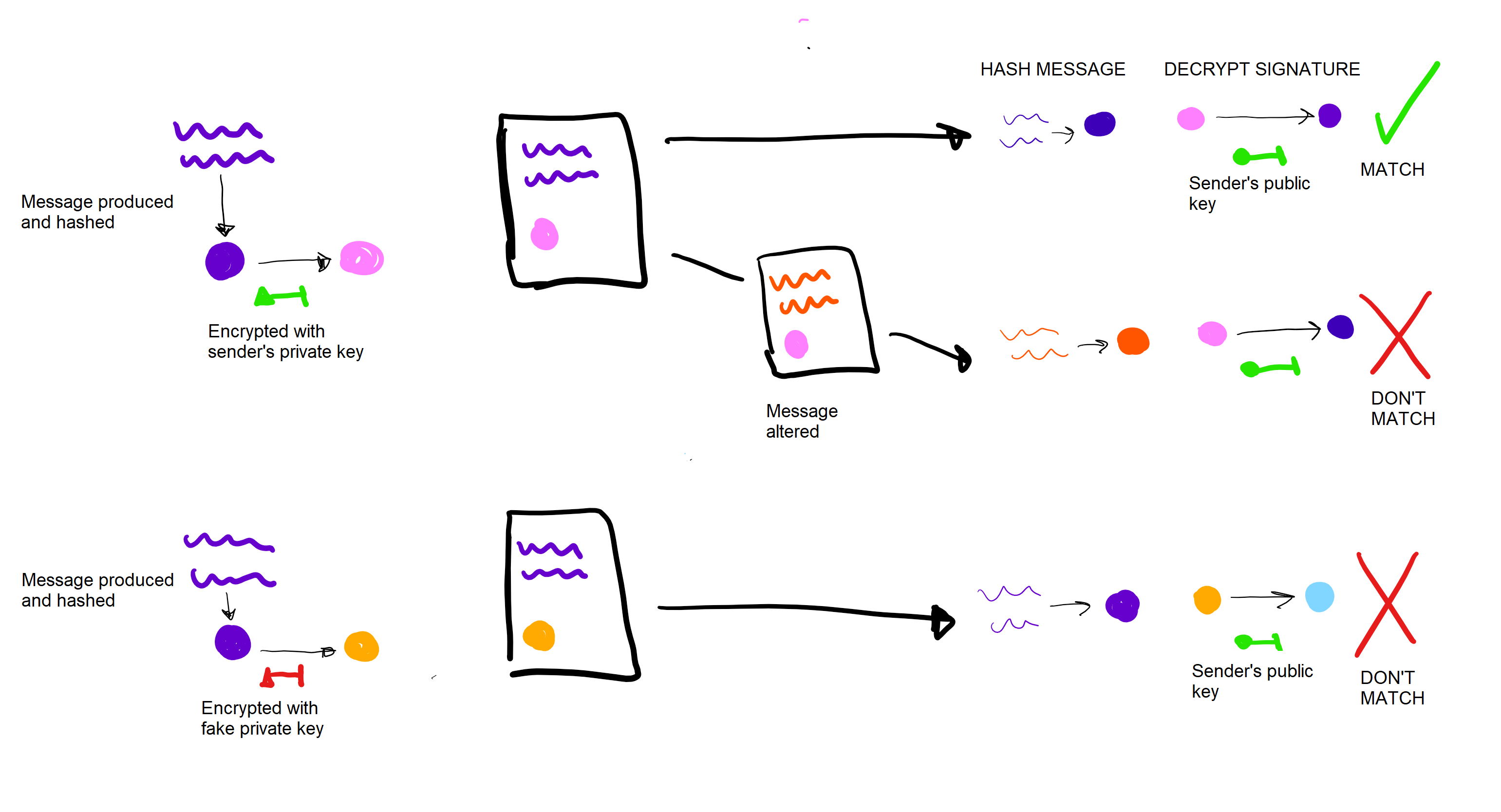
Now, say you had an important message you wanted to send to someone. The receiver needs to be able to firstly verify that you were the one that sent it, and secondly establish that the message has not been tampered with. Both aims can be achieved using asymmetric cryptography.
To "sign" a message, you produce a hash of the message, and then encrypt that hash with your private key. The receiver then runs the hash algorithm on the message, and then decrypts the signature with the public key. Decrypting the signature should produce what the sender originally encrypted, i.e. the hash of the message. Therefore, the two should match. If they do not, then either the message has been tampered with so the hash has been altered, or it was not produced with the sender's private key.
(A side note – something I find really interesting is quantum cryptography. Because, though incredibly difficult, breaking these mathematical encryptions is theoretically possible. However, using quantum encryption you could encrypt something using a truly unpredictable key, which is irrevocably altered in the presence of an unwanted observer.)
Blockchain
This is currently a real buzzword in the data community, and for good reason. It is the technology on which Bitcoin is based, but its possible applications beyond this are huge. The main ideas behind Blockchain are the verification of packets of information (like transactions, or edits) to produce a consistent and secure system. I'm going to base this example on Bitcoin, but I want to stress that there are many applications outside of cryptocurrency. A secure and consistent system has applications in many industries, and is hugely exciting for data management as a whole.
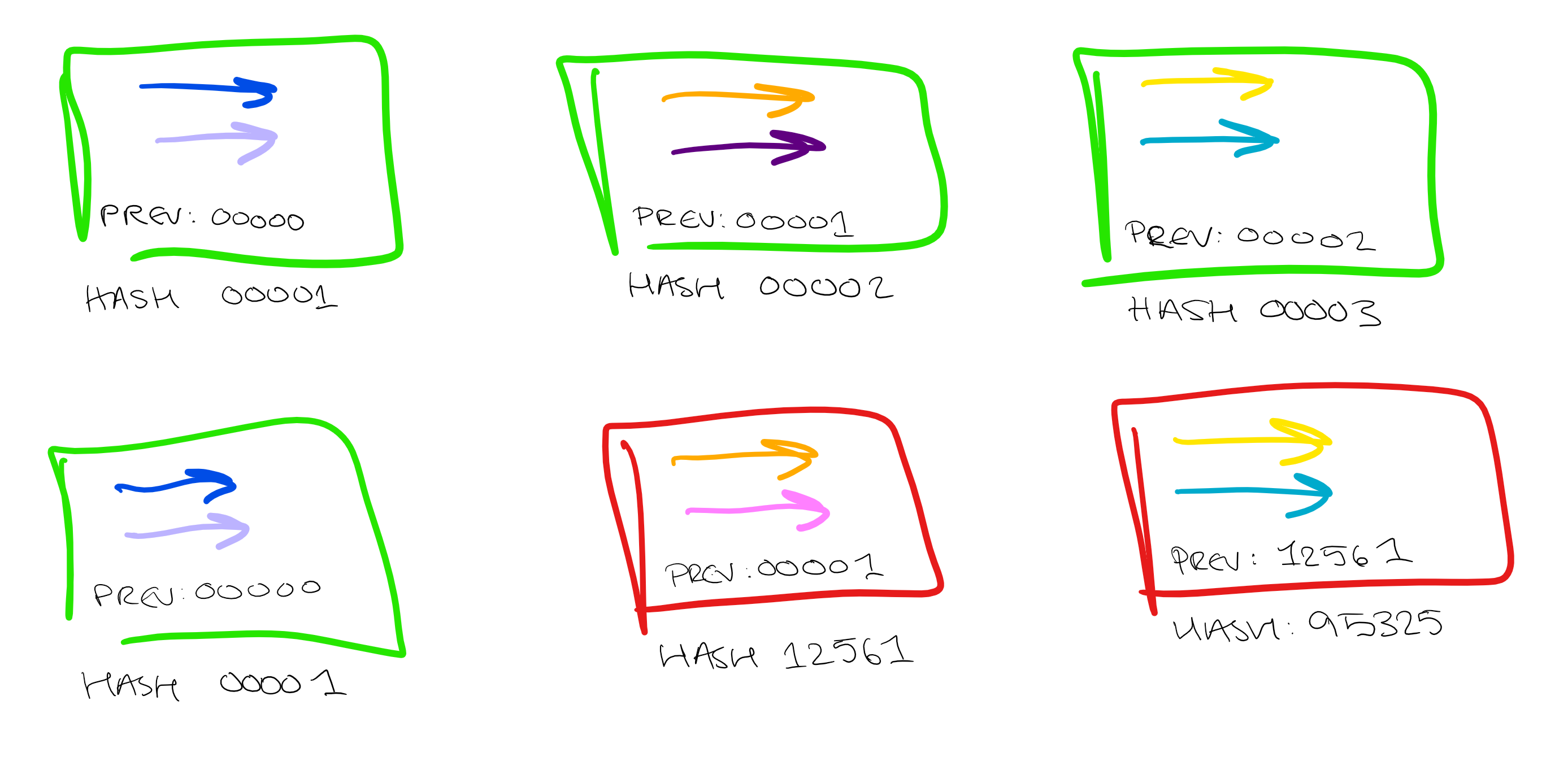
So, in Bitcoin, when someone attempts a transaction they sign that transaction with their private key and the receiver's public key and release it into the public sphere. "Miners" then group together a block of transactions do some work to validate that block. Each block includes a "nonce". This is just a number which accompanies that block of transactions. Each block also includes the validated hash of the previous set of transactions, forming a "chain". The miner then hashes the block and begins to "mine" it. This means involves changing the nonce, which in turn changes the hash, until the hash meets some predetermined condition.
or example, if the block of transactions:
Produced the hash:
b452f6e2-d152-456d-a8bb-402bcf525e4b
And the validation condition was such that the hash starts with four 0s. The nonce would then be changed until this condition was met. If the hashing algorithm used meant that a nonce value of 3000 meant that the hash was equal to:
0000124e-deb6-4989-b1f1-7982ccfa585d
then the miner would release this block into the public sphere, "validating" these transactions. The process of mining is an example of proof of work. The purpose of this is for the miner to confirm that they are invested in the block being validated. This is important because if two miners validate two blocks of inconsistent transactions at the same time, then the chain will fork. One of these chains will then have to be chosen as "the" chain. Mining provides a way to achieve this:
Miners in the community will need to base the blocks of transactions they subsequently mine on one of the two possible chains. They do this by choosing the longer chain, as more work has gone into validating it so there are more people invested in this being chosen as the "true" chain. In this way, one chain will continue to gain ground on the other and eventually any transactions in the chain that is not chosen will be invalidated. Because of this, it is common practice to wait until transactions are 6 blocks deep in the chain before acting upon them. In general this takes about an hour, as the goal for the length of time taken to mine a block is 10 minutes. This is a goal, as the algorithm is constantly monitoring the rate at which transactions are validated, and adjusts the difficulty of the puzzle accordingly. After 6 blocks, it is extremely unlikely that the transactions will be invalidated as too much work has been put into validating this branch of the chain.
Because of the work required to validate transactions, some incentive also has to be provided for mining. In BitCoin this is done by rewarding the miner who validates a block. They themselves receive some BitCoin, either from a coin-base, or from fees accompanying the transactions. The incentive for people to include fees with their transactions, is that a miner is more likely to include transactions with accompanying fees in their block, so your transaction is more likely to be validated.
Blockchain also provides protection against tampering. Each link in the chain also includes the hash of the previous block, so any attempt to tamper with the transactions will be immediately obvious. If any value is changed in any single transaction within a block, then the hash will be altered, which alters every subsequent hash in the chain, immediately invalidating the blocks. In this way the transaction chain is securely immutable.
Consistency and immutability, not bad from a data management perspective!
I hope you have enjoyed my brief dive into the world of encryption. I have a lot more depth to cover before being able to implement any of these concepts myself, but I feel I've gained a real appreciation for the sophisticated systems involved in keeping my data safe. And, though I'm not about to go and make any bitcoin-based investments, I find it very interesting to know how it all works. Guess that's another of my mental images that may need some updating…





